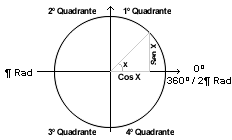
Trigonometria - Funções

Com base na figura ao lado, podemos concluir o
seguinte:
- Cada 180º equivalem a ¶ radianos;
- O seno de x aumenta conforme x aumenta;
- O cosseno de x diminui conforme x aumenta;
- O seno de x seria negativo no 3º e 4º quadrantes;
- O cosseno de x seria negativo no 2º e 3º quadrantes.
Seno
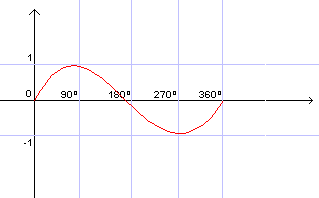
| Seno | Sinal | Cresc./Decresc. |
| 1ºQ | + | C |
| 2ºQ | + | D |
| 3ºQ | - | D |
| 4ºQ | - | C |
O período da função mostrada é 2¶ (360º, ou seja, onde o gráfico
termina).
A imagem da função representada é [-1;1].
Pode ser representada por f(x) = sen x.
Cosseno
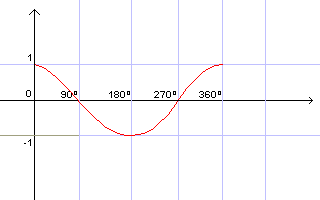
| Cosseno | Sinal | Cresc./Decresc. |
| 1ºQ | + | D |
| 2ºQ | - | D |
| 3ºQ | - | C |
| 4ºQ | + | C |
O período da função mostrada é 2¶ (360º, ou seja, onde o gráfico
termina).
A imagem da função representada é [-1;1].
Pode ser representada por f(x) = cos x.
Ex.: Sendo x um arco do 2º quadrante e sen x = 4/5, quanto vale cos x?
 (4/5)²
+ cosx² = 1² (Pitágoras. O raio vale sempre 1.)
(4/5)²
+ cosx² = 1² (Pitágoras. O raio vale sempre 1.)
16/25 - 1 = -cosx² (Isola-se o cosx². Resolve-se o que for
possível.)
16/25 - 25/25 = -cosx²
-9/25 = -cosx²
9/25 = cosx² (Multiplica por -1.)
cosx = 3/5 (Passa o expoente como raíz.)
cosx = -3/5 (ATENÇÃO: O SINAL DO RESULTADO É NEGATIVO, POIS O ARCO SE
ENCONTRA NO 2º QUADRANTE, ONDE O COSSENO É SEMPRE NEGATIVO, VERIFICANDO
AS TABELAS ACIMA.)
Resposta: -3/5
Período
Ex.: f(x) = sen (2x)
2x = 2¶ (Pega-se apenas x e seu
coeficiente e iguala-se a 2¶.)
x = 2¶/2
x = ¶
Resposta: O período de sen (2x) vale ¶.
Imagem
Ex.: f(x) = 3 cos x
[-1.3+0;1.3+0] (Pega-se o módulo do
coeficiente de cos x, multiplica-se pelo começo e fim da imagem padrão, que
são -1 e 1 e soma-se qualquer termo independete existente, no caso 0.)
[-3;3]
Resposta: A imagem de 3 cos x é
[-3;3].
Ex.: f(x) = -2 -3senx
[-1.3-2;1.3-2]
[-5;1]
Resposta: A imagem de -1 - 3 sen x é
[-5;1] (e é inversa, devido ao sinal do 3).
Representação gráfica
 Ex.:
3 -2sen(x/2)
Ex.:
3 -2sen(x/2)
Período: 4¶ (x/2=2¶)
Imagem: [1;5] (2.-1+3;2.1+3)
Inversa (inicia decrescente) devido ao
sinal negativo de 2.